반가산기(half-adder, HA)
반가산기란 한 자리 2진수 2개를 입력하여 합 S(Sum)과 캐리 C(Carry, 자리올림)를 계산하는 덧셈 회로이다.
출력 캐리(Cout)는 있지만 입력 캐리(Cin)는 없다.
예시로는 다음과 같다.
A 0 0 1 1
+ B + 0 + 1 + 0 + 1
--- --- --- --- ---
C S 0 0 0 1 0 1 1 0
위의 상황을 진리표로 표현하면 이렇다.
| 입력 | 출력 | ||
| A | B | S | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
이를 통해 논리식을 작성하면
S = A'B + AB' = A ⊕ B
C = AB
가 된다.
이를 통하여 논리회로를 작성해 보자.

논리 기호로는 이렇게 사용한다.

전가산기(full-adder, FA)
전가산기란 반가산기와 달리 자리 올림수(carry)를 고려하여서 만든 덧셈 회로이다.
출력 캐리와 입력 캐리가 모두 있다. 다음은 모든 경우의 수이다.
Ci 0 1 0 1 0 1 0 1
A 0 0 1 1 0 0 1 1
+ B + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1
---- --- --- --- --- --- --- --- ---
Co S 0 0 0 1 0 1 1 0 0 1 1 0 1 0 1 1
진리표를 작성하자.
| 입력 | 출력 | |||
| A | B | Ci | S | Co |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
논리식을 작성하자.

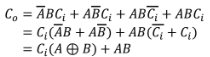
논리회로

반가산기로 치환할 수도 있다.

병렬 가감산기(parallel-adder/subtracter)
n개의 전가산기를 병렬로 연결하면 n비트 병렬 가산기를 얻을 수 있다.
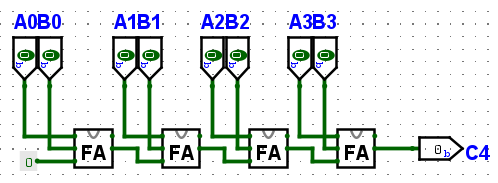
여기에 보수기를 결합하면 n비터 병렬 가감산기를 얻을 수 있다. B입력을 부호 S(sign)와 XOR하여 전가산기의 입력으로 사용해서 덧셈과 뺄셈이 모두 가능하다. S = 0일때 가산기의 역할을 하고, S = 1이면 B의 값이 반전 되어 1의 보수가 되고, S = 1이 캐리 입력 C0이 되어 결과적으로 1이 더해져서 2의 보수가 만들어진다. 따라서 감산기 역할을 한다.
고속 가산기(high-speed-adder)
고속 가산기 또는 캐리 예측(CLA: Carry Look Ahead) 가산기는 미리 캐리를 예측하여 가산 결과를 출력하는 가산기다.
기존의 병렬 가산기는 아래에서 위로 전달되는 캐리 때문에 속도가 느리다는 단점이 있었다. 이를 해결하고자 캐리 예측 가산기를 사용한다.
캐리 예측은 어떻게 할까? 캐리가 발생하는 경우는 두가지가 있다. 첫 번째는 합해지는 두 수 A, B 모두 1일때이다. 논리식으로는 AB이며 이를 G(올림수 생성, generate)로 치환한다. 두 번째는 A, B 중 하나가 1이고 밑에 자리에서 올라온 캐리 C가 1일 때이다. 논리식으로는 (A ⊕ B)C이며 (A ⊕ B) 를 P(올림수 전파, propagate)로 치환한다. 이 두 경우 중 하나만 해당하면 캐리가 발생하므로 캐리에 대한 논리식은 (이때 이 자릿수에서 발생한 캐리와 아래에서 발생한 캐리를 구분하기 위해 인덱스를 쓴다)
Ci+1 = AB + (A ⊕ B)Ci = G + PCi이다.
이를 통해 4비트 가산기에서의 식을 써보자.
C1 = G0 + P0C0 = G0 (C0이 0이므로)
C2 = G1 + P1C1 = G1 + P1G0
C3 = G2 + P2C2 = G2 + P2G1 + P2P1G0
C4 = G3 + P3C3 = G3 + P3G2 + P3P2G1 + P3P2P1G0
즉, 올림수 생성이 일어나거나, 혹은 아래자리에서 일어난 올림수 생성이 올림수 전파를 통해 윗자리까지 전달되는 경우의 합이다.
BCD 가산기
BCD코드는 2진수와 다르게 0에서 9까지만 표현한다. 따라서 1010에서 1111이 나오면 0110을 더하여 자릿수를 올려줘야 한다.
BCD 가산기는 합산 결과가 9를 초과하면 6을 더해 보정하는 회로가 부가된 4빝트 병렬 가산기이다.
'논리회로' 카테고리의 다른 글
| 멀티플렉서 완전 정리: 2×1부터 16×1 구성까지 한눈에 이해하기 (0) | 2025.05.11 |
|---|---|
| 인코더(Encoder) 정리: 2×1, 4×2 구조와 논리식까지 한눈에 이해하기 (0) | 2025.05.11 |
| 디코더와 디멀티플렉서 : 1×2, 2×4 구조와 논리식까지 (0) | 2025.05.11 |
| 비교기(Comparator) 완전 정리: 1비트부터 4비트까지 크기 비교 회로 이해하기 (0) | 2025.05.11 |
| 논리회로 기초 이론 정리 (진리표, 논리식, 설계 과정) (0) | 2025.05.09 |